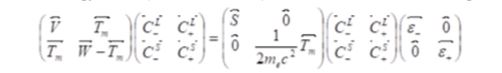Multicenter molecular integrals over dirac wave functions for solving the molecular matrix dirac equation

Title : Multicenter molecular integrals over dirac wave functions for solving the molecular matrix dirac equation

Abstract:

The gauge-invariant matrix Dirac equation was derived by Yoshizawa [1] as given by
    (1)
where   and   are the coefficient matrices for the large component spinor,   and   are those for the small component spinor,   and   are the energy matrices,   is the zero matrix, and the other matrix elements are given by
                             
in which   is a proper basis set,   is the Pauli spin matrices,   is the momentum,   is the vector potential of the magnetic field due to the nuclear spin , and   is the scalar potential. We use the Gauss-type charge density distribution (GCDD) model [2] for the vector potential of the magnetic field due to the finite nucleus, because some experiments show that the nucleus is not the point charge but a finite nucleus [2] and the GCDD model is frequently used for several calculations [3-5]. We use the atomic units throughout the present report ( ,  ,  ,  ,  ). However, we describe  ,  , and   explicitly for the readers convenience when one converts the units to the natural units. Using the Dirac identity, we have
            (6)
and
       (7)
Equation (6) shows necessary physical quantities in Eq. (3). Equation (7) does those in Eq. (4). Equations (2)-(5) show all of necessary matrix elements for solving the Dirac equation. 
Many researchers extend the matrix Dirac equation to the molecule [3-20]. For a molecule, the scalar potential may be the sum of one and two electron terms as given by
        (8)
where we use the GCDD model for the nuclear attraction. The Breit interaction [21] is not considered in the present report. Generally speaking, each matrix element is the multicenter molecular integral. It is natural to use the atomic Dirac wave function as the basis function for solving the molecular Dirac equation. However, there is no molecular integral formula for that purpose. The author derived the Gaussian-transform for the Dirac wave function centered at A in order to evaluate all of necessary molecular integrals as given by [22]. 
  
   (9)
where   in which   is the fine structure constant and   in which   is the nuclear charge. This Gaussian-transform is the only one formula to be able to evaluate the multicenter integral over Dirac wave functions. Using the formula, we can derive all necessary molecular integrals for solving the Dirac equation. Such will be presented in the conference.

Biography:

Dr. Ishida joined the research group of Prof. Teijiro Yonezawa at the Kyoto University in 1970. He received his PhD degree in 1975 at the same university. After one year postdoctoral fellowship supervised by Prof. Keiji Morokuma at the Rochester University, New York, he obtained the position of a lecturer at the Science University of Tokyo. He was retired from the university in 2011. He has published more than 30 articles in science journals. For example, most important three articles are listed below:
[1] K. Ishida, “Core radial polarization and the contact hyperfine structure of 4S state of nitrogen”, Phys Rev A12 (1975) 1153-1158.
[2] K. Ishida, “Calculus of several harmonic functions”, J Comput Chem Jpn. Int. Ed. 8 (2022) 2021-0029.
[3] K. Ishida, “Gaussian-transform for the Dirac wave function and its application to the multicenter molecular integral over Dirac wave functions for solving the molecular matrix Dirac equation”, IgMin Res. November 04 2024; 2(11): 897-914.